Amplification Audiophile et DIY
Haut-parleur (et enceinte)
Le logiciel Mathcad 6.0 ici utilisé, permet d'éditer en lien direct variables, équations et graphes. Un outil fort didactique pour accompagner les ouvrages d'électroacoustique. C'est une ancienne version, vers 1995.
Une version actuelle limitée en fonctions mais gratuite, peut être téléchargée sur le site de PTC.
Le fichier Mathcad en copies d'images ci-après est à disposition par mail. Il permet à partir des sept paramètres fondamentaux du haut-parleur sujet, d'obtenir la courbe du rayonnement sonore dans l'hémisphère qui lui fait face. La membrane est idéalisée à un piston plan et rigide de surface "Sd", monté en charge close. Les calculs sont déduits de ce schéma équivalent par analogie électrique / mécanique :
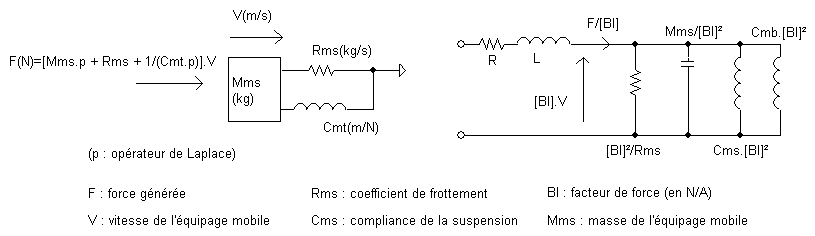
Le volume "V" est à saisir en litres. Quand le baffle est infini, "V" vaut également l'infini. Le niveau électrique "Unom" de 2,83 volts, donne le watt nécessaire à dimensionner la sensibilité normalisée. On pourra augmenter ce niveau pour comparer le déplacement induit au "Xmax" fourni par le constructeur. L'impédance interne "Rg" de l'amplificateur est à renseigner, zéro ohm pour les habituels amplis de tension. "d" est la distance où est calculé le niveau acoustique.
Au final, douze paramètres sont à renseigner : R, L, Bl, Sd, Rms, Mms, Cms, V, Xmax, Unom, Rg et d puis le fichier calcule l'ensemble des résultats. Ici, le haut-parleur Seas CA18RNX est pris en exemple.
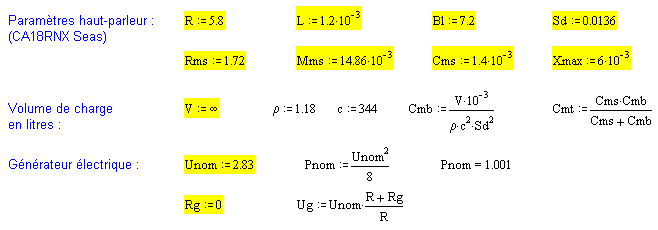
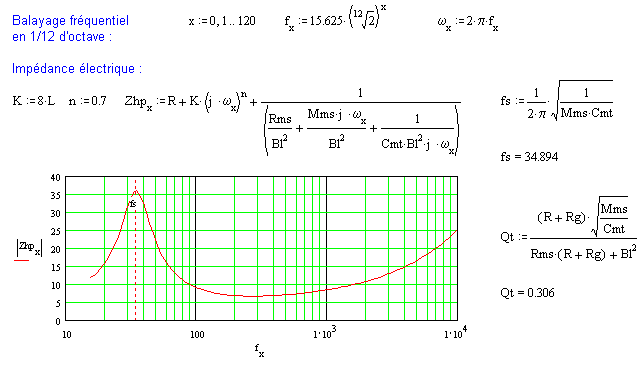
La valeur de l'inductance L à la bobine est mesurée par le constructeur généralement à 1kHz, or elle est variable avec la fréquence. Pertes par courant de Foucault et effet de peau dans le circuit magnétique sont en causes. W. Marshall Leach propose une modélisation proche d'une semi-inductance. L'impédance jLω devient K(jω)n où K et n sont à optimiser pour que la simulation s'approche au mieux de la courbe fournie.
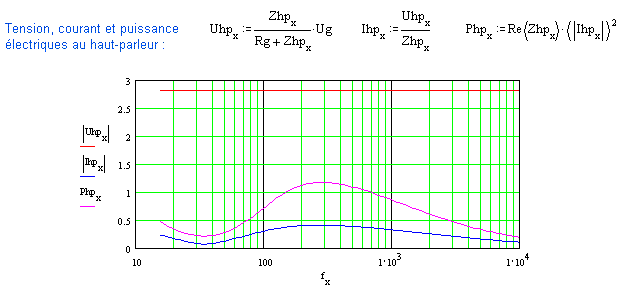
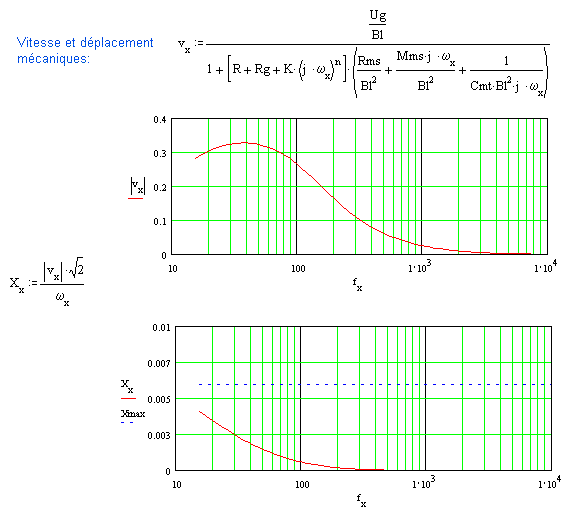
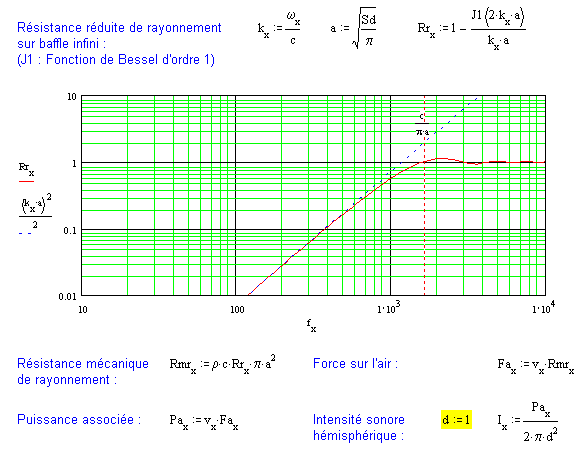
Quand en pratique le baffle plan infini devient un coffret de dimensions finies, le rayonnement devient progressivement sphérique plutôt qu'hémisphérique sous une fréquence inversement proportionnelle à ces dimensions. L'impédance de rayonnement finit par être divisée par 2 dans la bande utile (-3dB) et la puissance acoustique finit par être divisée par 4π plutôt que par 2π stéradians (-3dB).
L'applicaton "Edge" de Svante Granqvist permet la simulation de cette perte par dispersion (jusqu'à -6dB) en même temps que la simulation de la diffraction par effet de bord.
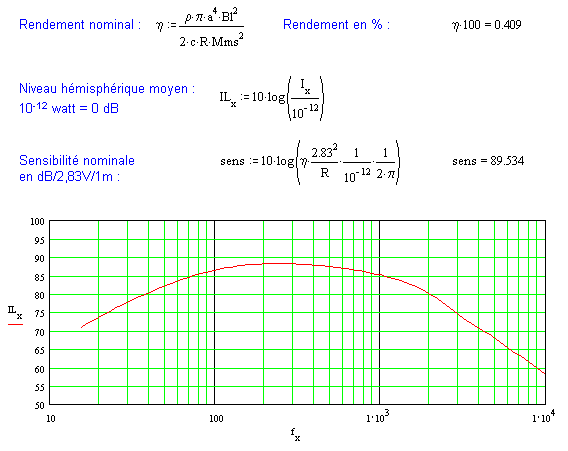
Il s'agit bien d'une réponse globale dans l'espace. Celle qui renseigne sur la capacité à alimenter la scène sonore et à ne pas dénaturer les timbres après réflexions sur les parois du local d'écoute. Une représentation qui peut aider à choisir la fréquence de coupure au filtre d'aiguillage.
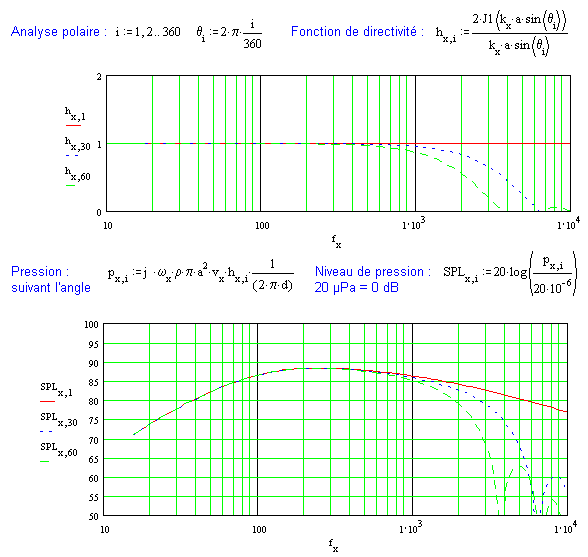
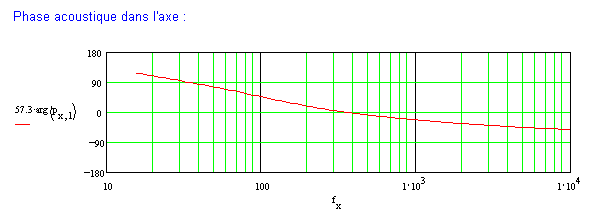
Ci-dessous une mise en formules qui permet un calcul de la réponse dans l'axe. Seul l'effet inductif considéré à la bobine mobile freine les aigus à partir du piston "parfait" (une self de 0mH donne une réponse axiale sans pente dans le haut du spectre). A 30° puis à 60°, on vérifie bien la chute en énergie.
 |
- - |  |
- - |  |
- - |  |
- - |  |